Concept for pathfinding

I don't need this yet because I don't have collision yet and I don't intend to add it so soon, but I want to write down the concept.

While my world itself is tile-based, movement in my game world isn't. Characters can move with floating point precision. I plan to use touchscreen/mouse as the primary input, so it would feel strange when they would be bound to 8-directional movement.

For that reason using A* using each tile as a node is not an option. But how can I do pathfinding in such an environment?

First I need to build a graph of nodes which have a direct line to each other:

1. Divide the world into rectangles which are either walkable or unwalkable. I wrote an article about how to do that for Manaserv.
2. Each corner of a walkable rectangle which borders at least one other walkable rectangle is a node.
3. Every node is also added to the other walkable rectangles it is adjacent to.
4. All nodes on the same rectangle are linked to each other. The weight of the links is the distance calculated by the Pythagorean theorem.
5. The nodes in step 4 are merged with the nodes they were created from, concatenating their lists of links. That way the linking between rectangles is made.

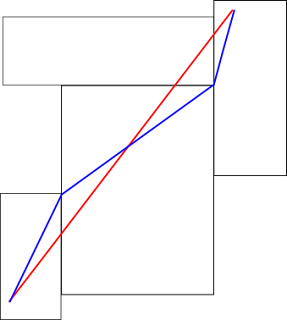I now have a graph of nodes which can be traversed without colliding with a wall. To get the start and end point into the graph, I just have to find out the rectangle they are in and calculate the distance to the nodes on that rectangle.

So how does the pathfinding work? I can just use Dijkstra's algorithm for finding the shortest list of nodes from A to B. This will give me a short route, but one which very likely has still room for improvement, because it will only allow me to move from rectangle to rectangle at the corner points (blue lines). When there would be a straight line (red line), this solution might be suboptimal.

But how do I get from the blue line to the red one?

I just traverse the nodes of my path, and look if there is a direct line of sight between the previous node and the next node. When there is, I replace the current node with a direct connection between the two (Are there cases where I need to repeat that multiple times? I am not sure...). Afterwards I should have a direct line where possible and a very naturally-looking path.

Finding out whether a line collides with a rectangle can be found out by checking if it intersects its diagonals (assuming both ends of the line are outside of the rectangle, which can be assured in this case). Line intersection can be implemented using this algorithm.

Preloading Images